Footsteps Planning: Step-by-Step Guide

A comprehensive guide to footstep planning for bipeds and quadrupeds, covering 2D and 3D foot trajectories, ZMP generation, and CoM trajectory computation.

Leonardo BertelliLeonardo Bertelli
••20 minutes
Footsteps Planning: Step-by-Step Guide
Argo-Robot/footsteps_planning

GitHub - Argo-Robot/footsteps_planning

Learn how to design a footstep planner for humanoid robots, breaking down the entire process step by step: 2D footsteps planning, 3D feet trajectory generation, ZMP and CoM trajectory generation.

GitHubArgo-Robot

Footstep planning is a fundamental component of locomotion for legged robots, allowing them to move efficiently and adaptively in complex environments. Whether it’s a biped navigating a cluttered household or a quadruped traversing uneven terrain, this process involves generating precise foot trajectories while considering the robot's dynamics and stability constraints.

Typically, the planning process consists of two stages:

  • Global Path Planning: This module computes a high-level path for the robot to follow, usually avoiding obstacles and determining a viable route.
  • Footstep Planning: Based on the global path, this step computes the exact placement of each foot to ensure the robot follows the intended trajectory.

Bipeds

Footstep planning for bipeds typically involves generating foot placements in both 2D and 3D spaces. In addition to foot placements, the trajectories of the robot’s Center of Mass (CoM) and the Zero Moment Point (ZMP) play a vital role in maintaining balance. The CoM trajectory ensures the robot's weight remains balanced, while the ZMP trajectory prevents tipping by maintaining stability during walking.

Note: All these reference trajectories (footsteps, CoM) will be then followed by a high-level tracking controller. However, the design and implementation of such a controller is beyond the scope of this article.

1) Global Trajectory

Global Trajectory

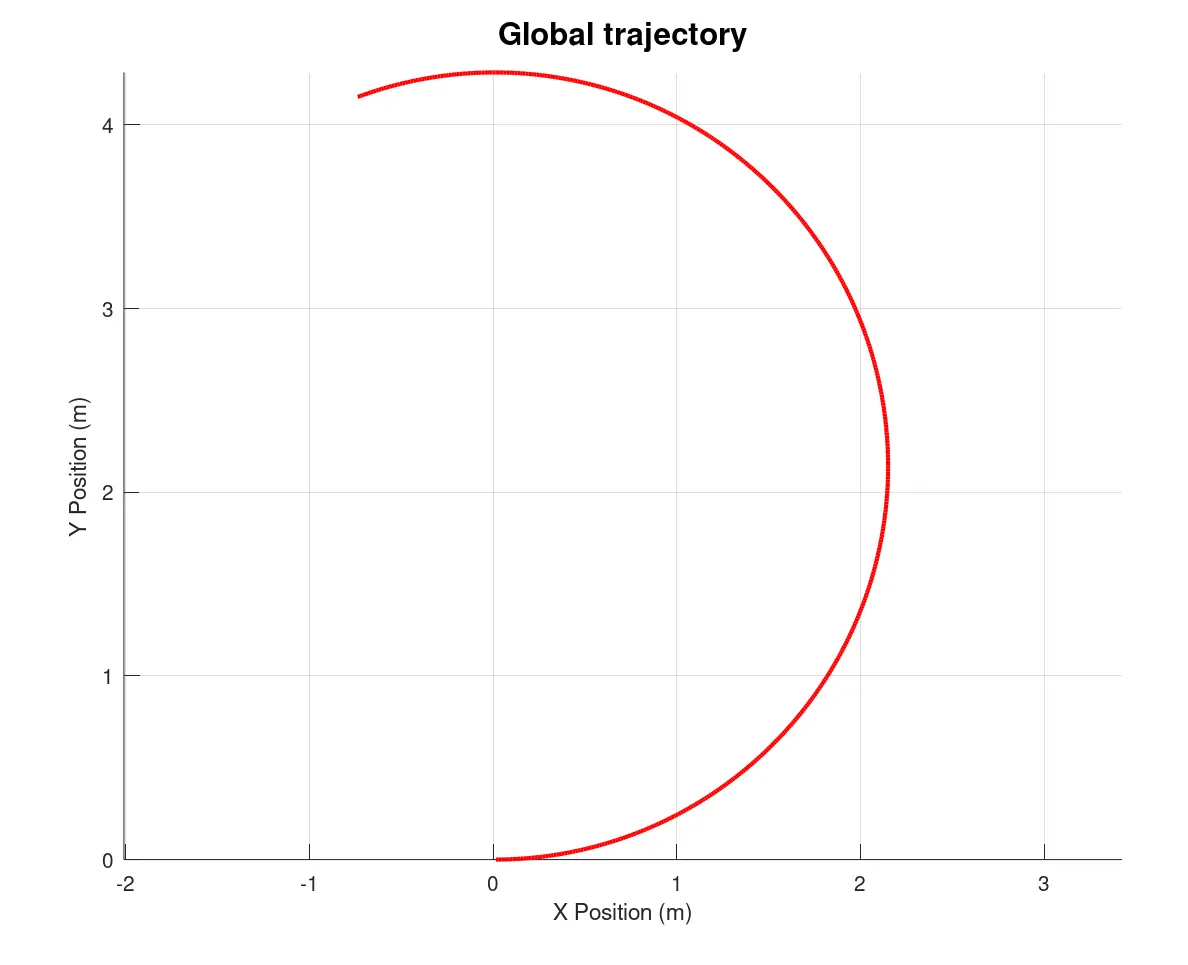
The global trajectory represents the motion of a robot from a starting location to a goal location, typically computed by a high-level planner. This planner generates an obstacle-free sequence of positions for the robot to follow.

However, in this example, we generate a simplified trajectory using just two primary inputs:

  • Linear velocity: The forward speed vv of the robot.
  • Angular velocity: The rate of rotation ww of the robot around its vertical axis.

Given these inputs, the robot’s trajectory can be computed over a time interval TT using small time steps of duration ΔT\Delta T. At each step, the position (x,yx, y) and orientation θ\theta are updated iteratively based on the following equations of motion:

  • xi+1=xi+vcos⁡(θi)ΔTx_{i+1} = x_i + v \cos(\theta_i) \Delta T
  • yi+1=yi+vsin⁡(θi)ΔTy_{i+1} = y_i + v \sin(\theta_i) \Delta T
  • θi+1=θi+wΔT\theta_{i+1} = \theta_i + w \Delta T

This method provides a simple way to simulate a global trajectory for navigation tasks.

2) 2D Footsteps Planning

2D Footsteps Planning

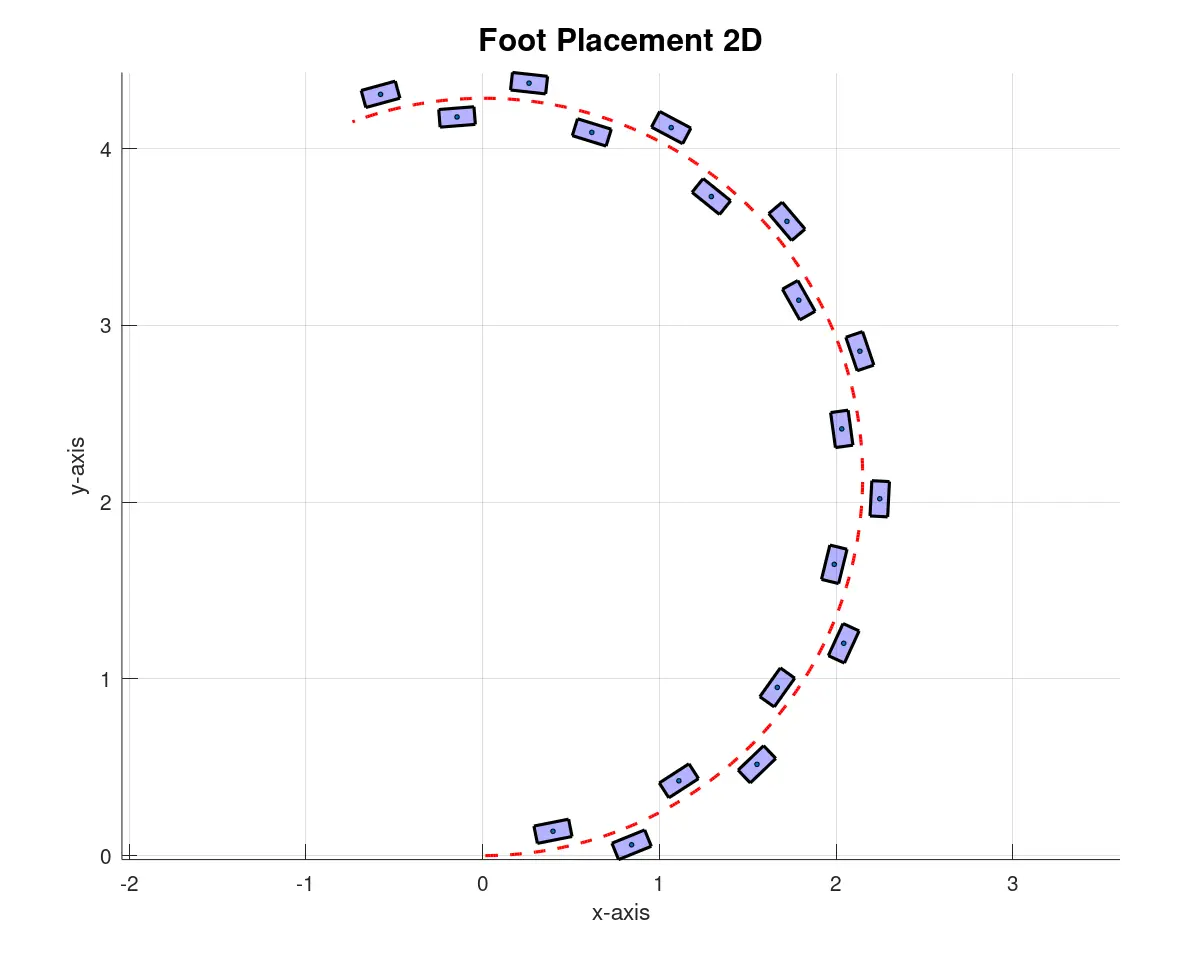
2D Footstep Planning involves generating precise foot placements around the global trajectory, alternating between the left and right foot. Key parameters include:

  • Step Length L: The forward distance between consecutive foot placements.
  • Step Width W: The lateral distance between the left and right feet.

Steps of the Algorithm:

  1. Tangent and Normal Calculation: At each point along the trajectory, a tangent vector t=[cos⁡(θ),sin⁡(θ)]\mathbf{t} = [\cos(\theta), \sin(\theta)] is computed to determine the robot’s direction of motion. The normal vector n\mathbf{n} is derived from the tangent to define lateral offsets for foot placement:
n=[−sin⁡(θ),cos⁡(θ)]\mathbf{n} = [-\sin(\theta), \cos(\theta)]
  1. Foot Placement: A new foot placement is added whenever the robot travels a distance equal to the step length LL. The position of the foot is calculated as:
xfoot=xtrajectory+W2⋅nx⋅(2⋅is_right_foot−1)x_{\text{foot}} = x_{\text{trajectory}} + \frac{W}{2} \cdot n_x \cdot (2 \cdot \text{is\_right\_foot} - 1)
yfoot=ytrajectory+W2⋅ny⋅(2⋅is_right_foot−1)y_{\text{foot}} = y_{\text{trajectory}} + \frac{W}{2} \cdot n_y \cdot (2 \cdot \text{is\_right\_foot} - 1)

The orientation of the foot is set to align with the tangent:

θfoot=arctan⁡2(ty,tx)\theta_{\text{foot}} = \arctan2(t_y, t_x)
  1. Alternating Steps: The algorithm alternates between placing left and right foot positions, ensuring symmetric gait patterns.

By following this approach, the robot can accurately generate a sequence of 2D foot placements that follow the global trajectory while adhering to step length and width constraints.

3) 3D Foot Trajectory Planning

3D Foot Trajectory Planning

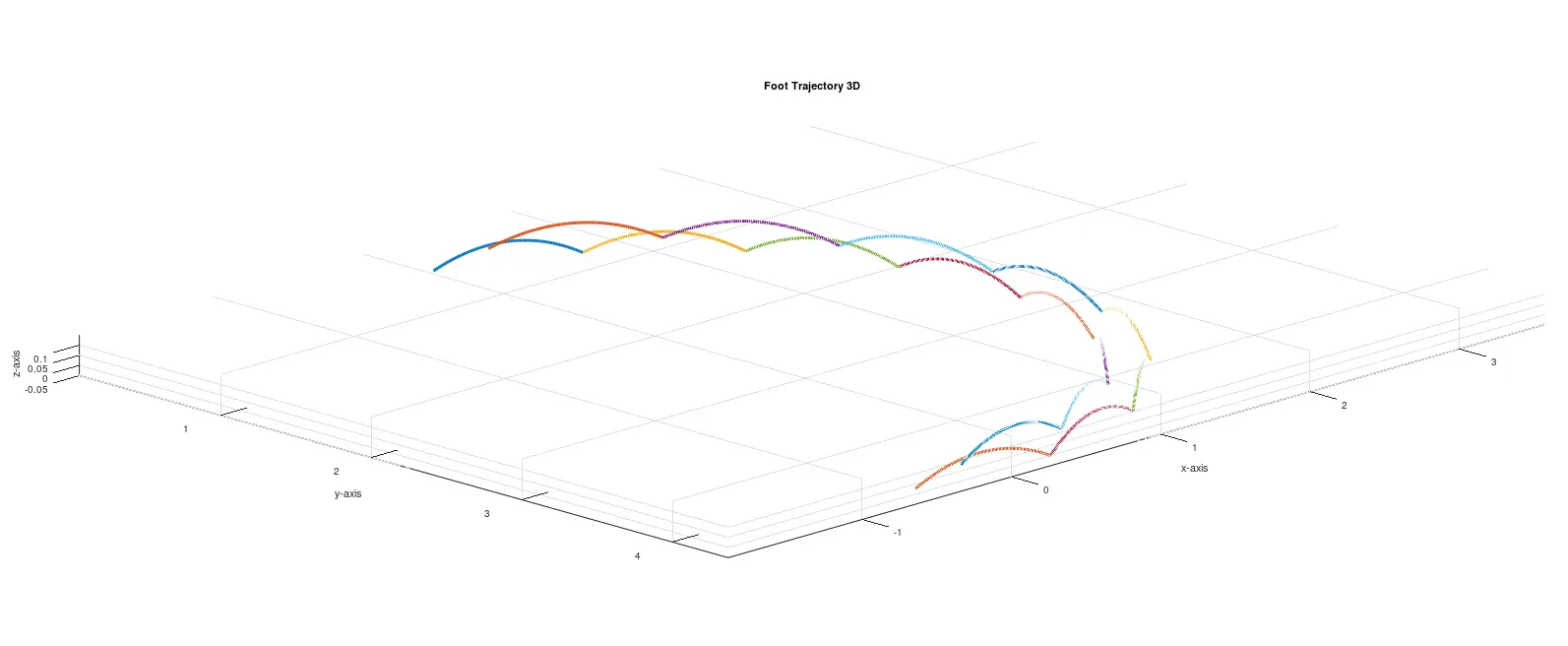
3D Foot Trajectory Planning extends the 2D footstep positions into a fully defined 3D trajectory, including height variations for each step.

Each step's trajectory is defined as a sequence of homogeneous transformations in 3D space, generated from the following elements:

  • 2D footsteps: The 2D feet positions generated from the previous step.
  • Step Height: The vertical lift of the foot, ensuring clearance over obstacles.
  • Step Time: The duration of each step.

Algorithm Steps:

  1. Time Normalization: Each single step trajectory is generated over a normalized time interval [0,1][0, 1], split into nn discrete steps:
t=linspace(0,1,n)t = \text{linspace}(0, 1, n)
  1. Interpolation for x, y Trajectory: The positions in the x−yx-y plane are interpolated between the start and end positions of the step using cubic splines:
xtraj(t)=interp(xstart,xend,t)x_{\text{traj}}(t) = \text{interp}(x_{\text{start}}, x_{\text{end}}, t)
ytraj(t)=interp(ystart,yend,t)y_{\text{traj}}(t) = \text{interp}(y_{\text{start}}, y_{\text{end}}, t)
  1. Parabolic z Trajectory: To ensure smooth lifting and landing, the zz-trajectory follows a parabolic profile:
ztraj(t)=4⋅H⋅t⋅(1−t)z_{\text{traj}}(t) = 4 \cdot H \cdot t \cdot (1 - t)
  1. Homogeneous Transformation Matrices: At each time step, the 3D foot position is represented as a homogeneous transformation matrix:
T(t)=[Rz(θ)p(t)01]T(t) = \begin{bmatrix} R_z(\theta) & \mathbf{p}(t) \\ 0 & 1 \end{bmatrix}

where:

  • Rz(θ)R_z(\theta) is the rotation matrix for the foot orientation around zz-axis:
Rz(θ)=[cos⁡(θ)−sin⁡(θ)0sin⁡(θ)cos⁡(θ)0001]R_z(\theta) = \begin{bmatrix} \cos(\theta) & -\sin(\theta) & 0 \\ \sin(\theta) & \cos(\theta) & 0 \\ 0 & 0 & 1 \end{bmatrix}
  • θ\theta is the foot orientation.
  • p(t)=[xtraj(t),ytraj(t),ztraj(t)]⊤\mathbf{p}(t) = [x_{\text{traj}}(t), y_{\text{traj}}(t), z_{\text{traj}}(t)]^\top is the 3D position of the foot.

This process generates a sequence of 3D foot placements that follow the global trajectory, by computing poth 3D positions and 3D orientations for each foot.

4) ZMP Trajectory Generation

ZMP Trajectory Generation

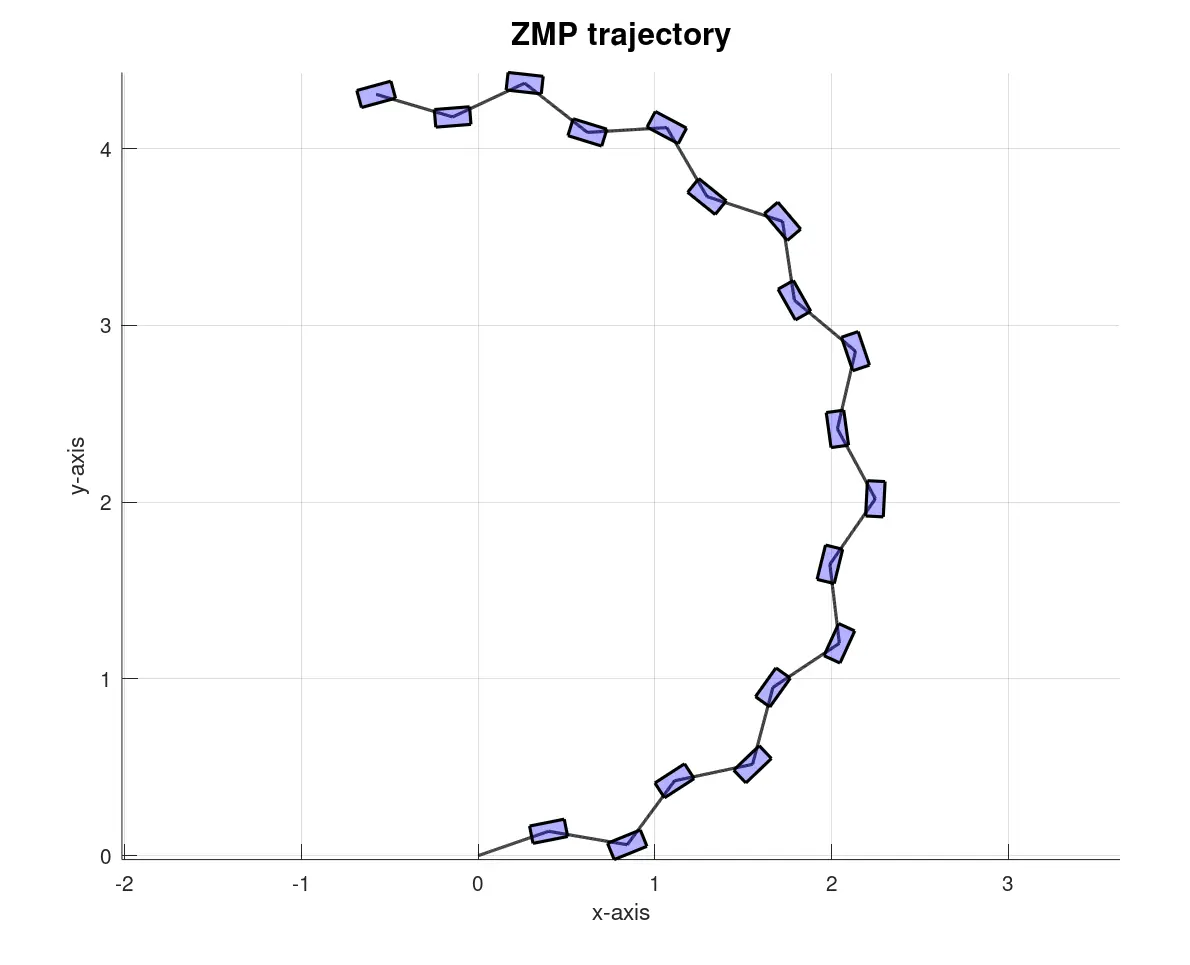
The Zero Moment Point (ZMP) is a critical concept in legged locomotion, serving as a stability indicator for robots. It represents the point on the ground where the resultant moment of forces, generated by gravity and inertia, equals zero. In simpler terms, the ZMP helps determine if the robot’s motion is dynamically stable. If the ZMP lies within the support polygon, the robot is stable and unlikely to tip over.

What is the Support Polygon?

The Support Polygon is the area enclosed by the contact points of the robot's feet with the ground. For example:

  • For a biped robot in a single support phase, the support polygon is the area under the single foot in contact.
  • For a biped in a double support phase, the support polygon is the area formed between both feet.

The ZMP must remain inside the support polygon to maintain stability. If it moves outside, the robot becomes unstable and risks falling.

ZMP Trajectory Generation

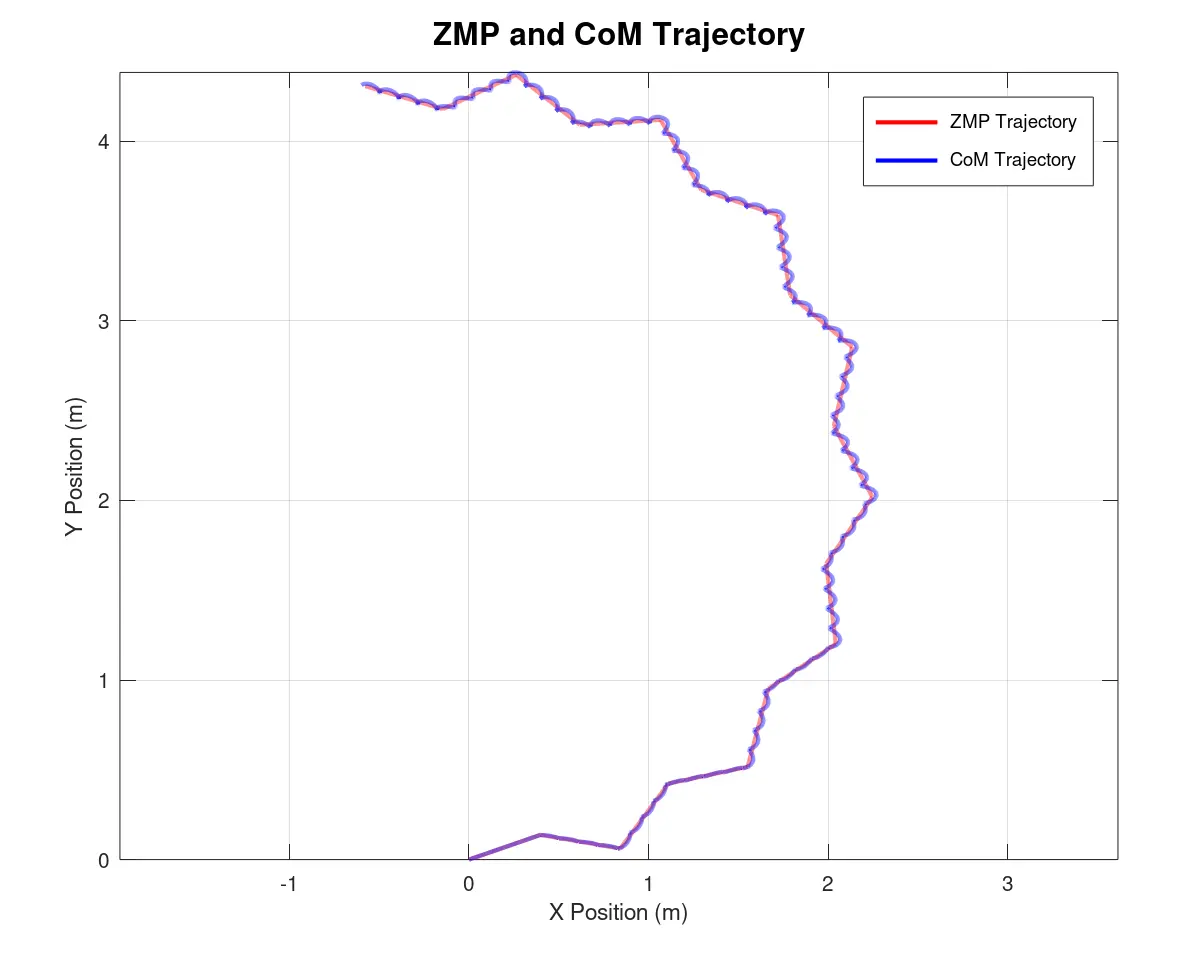
To generate a smooth and stable ZMP trajectory, the planned 2D footstep positions serve as the foundation. Using cubic spline interpolation, a continuous and smooth path is calculated between consecutive footstep positions. This interpolation method guarantees that the ZMP trajectory transitions naturally between steps without abrupt changes, maintaining stability. The resulting trajectory consists of a series of smooth points (xZMP,yZMP)(x_{\text{ZMP}}, y_{\text{ZMP}}) that lie within the support polygon, ensuring dynamic balance throughout the robot’s motion.

5) CoM Pelvis Trajectory Generation

The Center of Mass (CoM) trajectory plays a critical role in ensuring the robot remains dynamically stable during motion. We can procede in couple of ways to compute this reference.

5.1) Dynamics Relations with ZMP

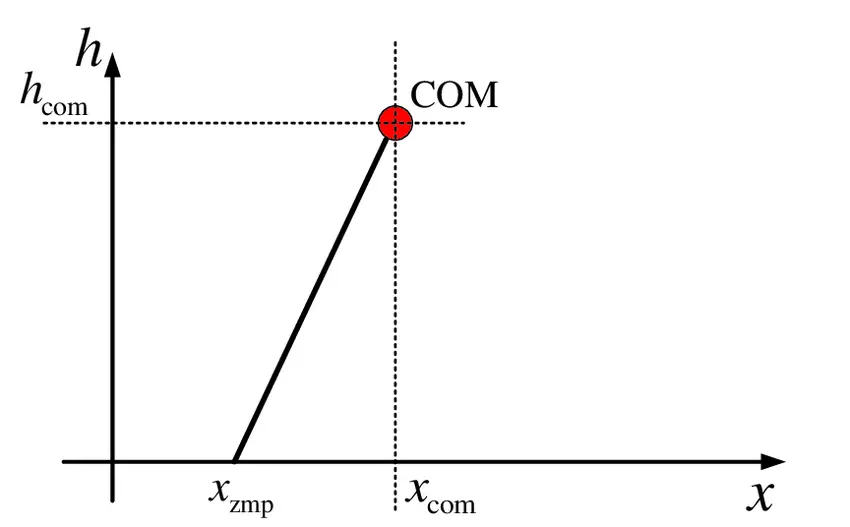
Global Trajectory

The CoM and the ZMP relationship can be expressed through the Linear Inverted Pendulum (LIP) model, which is a simplified dynamic representation of a robot's motion.

Linear Inverted Pendulum (LIP) Model

Linear Inverted Pendulum Model

The LIP model assumes the following:

  • The robot's mass is concentrated at its CoM.
  • The CoM moves at a constant height hh above the ground.
  • The contact forces act at the ZMP, which lies within the support polygon.
Global Trajectory

Using these assumptions, the horizontal CoM accelerations are directly related to the ZMP position. Indeed, recalling the ZMP definition (it represents the point on the ground where the resultant moment of forces equals zero), the following dynamic equations hold:

Myzmp=m⋅x¨CoM⋅zCoM−mg⋅(x˙CoM−xZMP)=0M_{y_{{zmp}}} = m \cdot \ddot{x}_{\text{CoM}} \cdot {z}_{\text{CoM}} - mg \cdot (\dot{x}_{\text{CoM}} - x_{\text{ZMP}}) = 0
Mxzmp=m⋅y¨CoM⋅zCoM−mg⋅(y˙CoM−yZMP)=0M_{x_{{zmp}}} = m \cdot \ddot{y}_{\text{CoM}} \cdot {z}_{\text{CoM}} - mg \cdot (\dot{y}_{\text{CoM}} - y_{\text{ZMP}}) = 0

Rearranging the equations, we obtain:

x¨CoM=gh(xCoM−xZMP)\ddot{x}_{\text{CoM}} = \frac{g}{h} (x_{\text{CoM}} - x_{\text{ZMP}})
y¨CoM=gh(yCoM−yZMP)\ddot{y}_{\text{CoM}} = \frac{g}{h} (y_{\text{CoM}} - y_{\text{ZMP}})

where:

  • x¨CoM\ddot{x}_{\text{CoM}} is the acceleration of the CoM in the xx-direction.
  • y¨CoM\ddot{y}_{\text{CoM}} is the acceleration of the CoM in the yy-direction.
  • xZMPx_{\text{ZMP}} and yZMPy_{\text{ZMP}} are the ZMP coordinates in the xx- and yy-directions.
  • gg is the gravitational constant.
  • hh is the constant height of the CoM above the ground.

Computation of CoM Trajectory

The CoM trajectory can be calculated iteratively using the ZMP trajectory as input. At each time step, the following steps are performed:

  1. Compute the CoM acceleration:
x¨CoM=gh(xCoM−xZMP)\ddot{x}_{\text{CoM}} = \frac{g}{h} (x_{\text{CoM}} - x_{\text{ZMP}})
y¨CoM=gh(yCoM−yZMP)\ddot{y}_{\text{CoM}} = \frac{g}{h} (y_{\text{CoM}} - y_{\text{ZMP}})
  1. Integrate the acceleration to update the CoM velocity (keep in mind it is an intertial acceleration):
x˙CoM=x˙CoM−x¨CoM⋅Δt\dot{x}_{\text{CoM}} = \dot{x}_{\text{CoM}} - \ddot{x}_{\text{CoM}} \cdot \Delta t
y˙CoM=y˙CoM−y¨CoM⋅Δt\dot{y}_{\text{CoM}} = \dot{y}_{\text{CoM}} - \ddot{y}_{\text{CoM}} \cdot \Delta t
  1. Integrate the velocity to update the CoM position:
xCoM=xCoM+x˙CoM⋅Δtx_{\text{CoM}} = x_{\text{CoM}} + \dot{x}_{\text{CoM}} \cdot \Delta t
yCoM=yCoM+y˙CoM⋅Δty_{\text{CoM}} = y_{\text{CoM}} + \dot{y}_{\text{CoM}} \cdot \Delta t

The resulting trajectory (xCoM,yCoM)(x_{\text{CoM}}, y_{\text{CoM}}) provides a smooth and stable path for the robot's Center of Mass, ensuring dynamic balance throughout the motion.

5.2) Open-Loop Sine Wave

Open-Loop Sine Wave

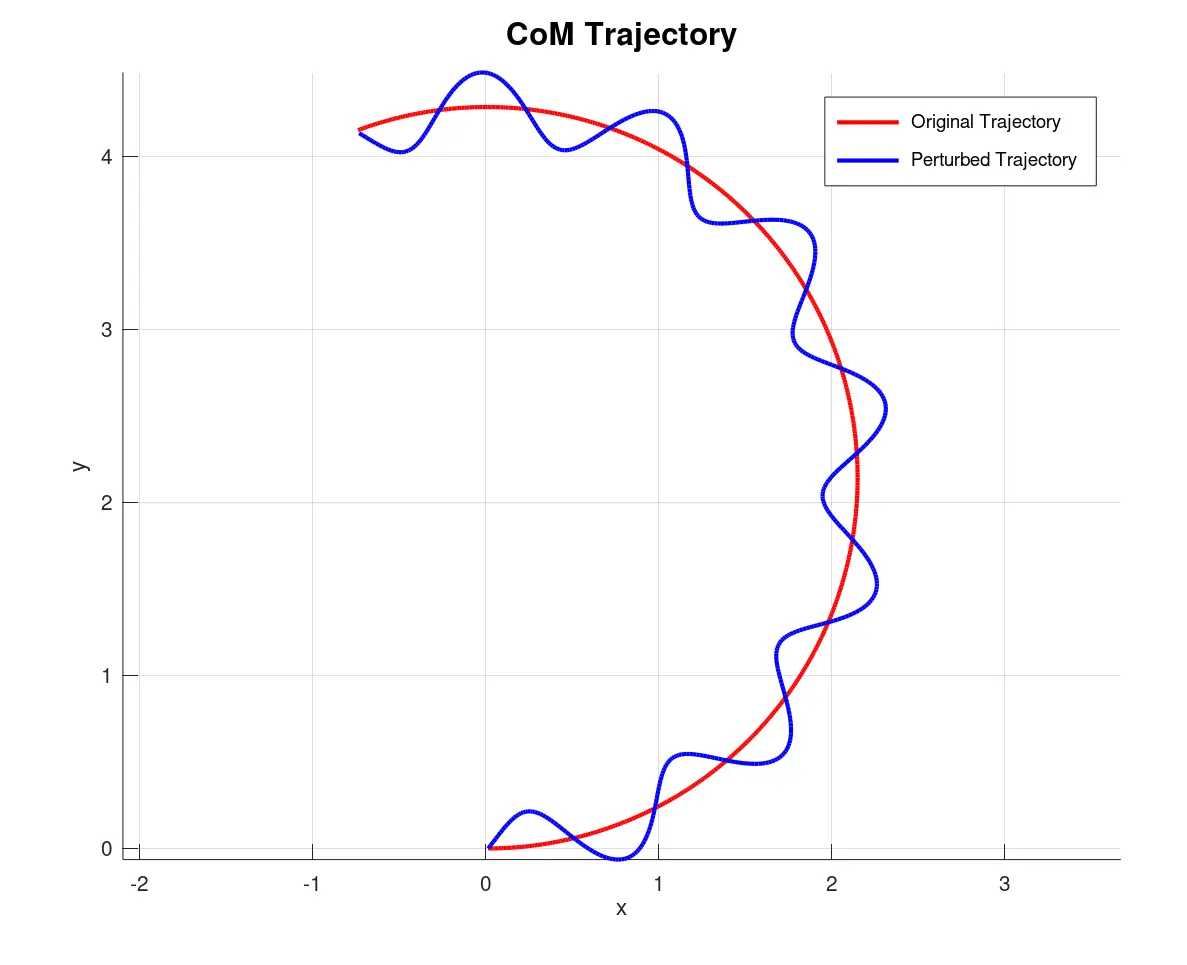
Another alternative to generate the CoM trajectory consists in introducing a sinusoidal perturbation around the global trajectory. This perturbation, added along the normal direction at each point, mimics the lateral oscillations observed in biological locomotion. While this approach doesn't derive directly from dynamic equations, it is inspired by the natural, rhythmic oscillations seen in biological systems.

Sinusoidal Perturbation Model

The sinusoidal perturbation is defined as:

s(t)=A⋅sin⁡(2πsarcλ)s(t) = A \cdot \sin\left(\frac{2 \pi s_{\text{arc}}}{\lambda}\right)

where:

  • AA: Amplitude of the sine wave, controlling the lateral deviation of the CoM.
  • λ\lambda: Wavelength of the sine wave, determining the frequency of oscillation.
  • sarcs_{\text{arc}}: The arc length along the robot's trajectory.

Generating the Perturbed CoM Trajectory

  1. Compute Arc Length: The arc length is computed incrementally along the trajectory as:
s(i)=s(i−1)+(x(i)−x(i−1))2+(y(i)−y(i−1))2s(i) = s(i-1) + \sqrt{\left(x(i) - x(i-1)\right)^2 + \left(y(i) - y(i-1)\right)^2}
  1. Tangent and Normal Vectors: At each point, the tangent vector t⃗\vec{t} is calculated as:
t⃗=∂p⃗∂s=(∂x∂s,∂y∂s)\vec{t} = \frac{\partial \vec{p}}{\partial s} = \left( \frac{\partial x}{\partial s}, \frac{\partial y}{\partial s} \right)

The normal vector n⃗\vec{n} is derived by rotating the tangent vector 90°:

n⃗=(−ty,tx)\vec{n} = (-t_y, t_x)
  1. Apply Perturbation: The sine wave perturbation is applied along the normal vector:
p⃗perturbed=p⃗global_trajectory+s(t)⋅n⃗\vec{p}_{\text{perturbed}} = \vec{p}_{\text{global\_trajectory}} + s(t) \cdot \vec{n}

This simpler approach generates an open-loop CoM trajectory, simulating oscillating gait patterns often observed in biological locomotion.

Quadrupeds

Quadrupeds, with their four-legged structure, offer inherent stability but require precise coordination between legs for smooth and efficient movement. Locomotion in quadrupeds is characterized by various gait patterns, each suited for specific speeds or terrains. Effective footstep planning for quadrupeds involves managing the "phase" of each leg’s movement, which refers to whether a leg is in the stance phase (in contact with the ground) or the swing phase (moving forward through the air).

Common Gait Patterns:

  • Walk: A slow, stable gait where legs move one at a time, ensuring at least three points of contact with the ground at all times.
  • Trot: A faster gait where diagonally opposite legs move together in pairs, offering a balance of speed and stability.
  • Gallop: A dynamic gait used for higher speeds, featuring a suspended phase where all legs are momentarily off the ground.

3D Foot Trajectory for Quadrupeds

3D Foot Trajectory for Quadrupeds

The 3D foot trajectory describes the path of each foot in three-dimensional space (x, y, z) throughout the gait cycle. For quadrupeds, we use an elliptical trajectory to represent the foot motion in the xz-plane:

footx(t)=Axcos⁡(ϕ(t))\text{foot}_x(t) = A_x \cos(\phi(t))
footz(t)=−Azsin⁡(ϕ(t))\text{foot}_z(t) = -A_z \sin(\phi(t))

Where:

  • AxA_x is the amplitude of the foot movement in the forward (x) direction.
  • AzA_z is the amplitude of the vertical (z) direction.

While ϕ(t)\phi(t) is the phase at time tt, and is defined as:

ϕ(t)=ϕ0+2πf0t\phi(t) = \phi_0 + 2 \pi f_0 t

Where:

  • ϕ0\phi_0 is the initial phase of the leg.
  • f0f_0 is the frequency of the gait.
  • tt is the time at which the foot trajectory is computed.

In our example, we choose to perform a Trot Gait. Thus, the legs move in a diagonal gait pattern, where the front left leg and the rear right leg move together, and the front right leg and rear left leg move together in the opposite phase. The phase shifts ϕ0\phi_0 between these legs are defined as:

  • Front Left Leg: ϕFL=0\phi_{\text{FL}} = 0
  • Rear Right Leg: ϕRR=0\phi_{\text{RR}} = 0
  • Front Right Leg: ϕFR=π\phi_{\text{FR}} = \pi (opposite phase to FL and RR)
  • Rear Left Leg: ϕRL=π\phi_{\text{RL}} = \pi (opposite phase to FL and RR)

This approach allows for precise control over the motion of each foot, enabling smooth and stable locomotion.

Key Works and Citations

Authors

Leonardo Bertelli

Leonardo Bertelli

View Portfolio
@article{leonardobertelli2025,
  author = {Leonardo Bertelli},
  title = {Footsteps Planning: Step-by-Step Guide},
  year = {2025},
  month = {January},
  day = {26},
  url = {https://federicosarrocco.com/blog/footsteps-planning}
}

Related Posts

Making quadrupeds Learning to walk: Step-by-Step Guide

Making quadrupeds Learning to walk: Step-by-Step Guide

Feb 4, 2025

Learn how to train a quadruped robot to walk using reinforcement learning, from defining actions and observations to designing rewards and transitioning from simulation to reality.

Unit Testing Robotic Software Components: Best Practices in C++

Unit Testing Robotic Software Components: Best Practices in C++

Apr 22, 2024

A comprehensive guide to writing effective unit tests for robotic software components, with practical examples and best practices in C++.

Flow Matching Explained: From Noise to Robot Actions

Flow Matching Explained: From Noise to Robot Actions

Nov 8, 2024

Learn how flow matching generates continuous data, such as robot actions, by denoising samples drawn from a simple noise distribution. Understand the key concepts, training process, and application in robotics.

Graph SLAM: From Theory to Implementation

Graph SLAM: From Theory to Implementation

Oct 26, 2024

A comprehensive guide to understanding and implementing Graph SLAM, covering theoretical foundations, mathematical principles, and practical implementation with real-world examples.